publications
2026
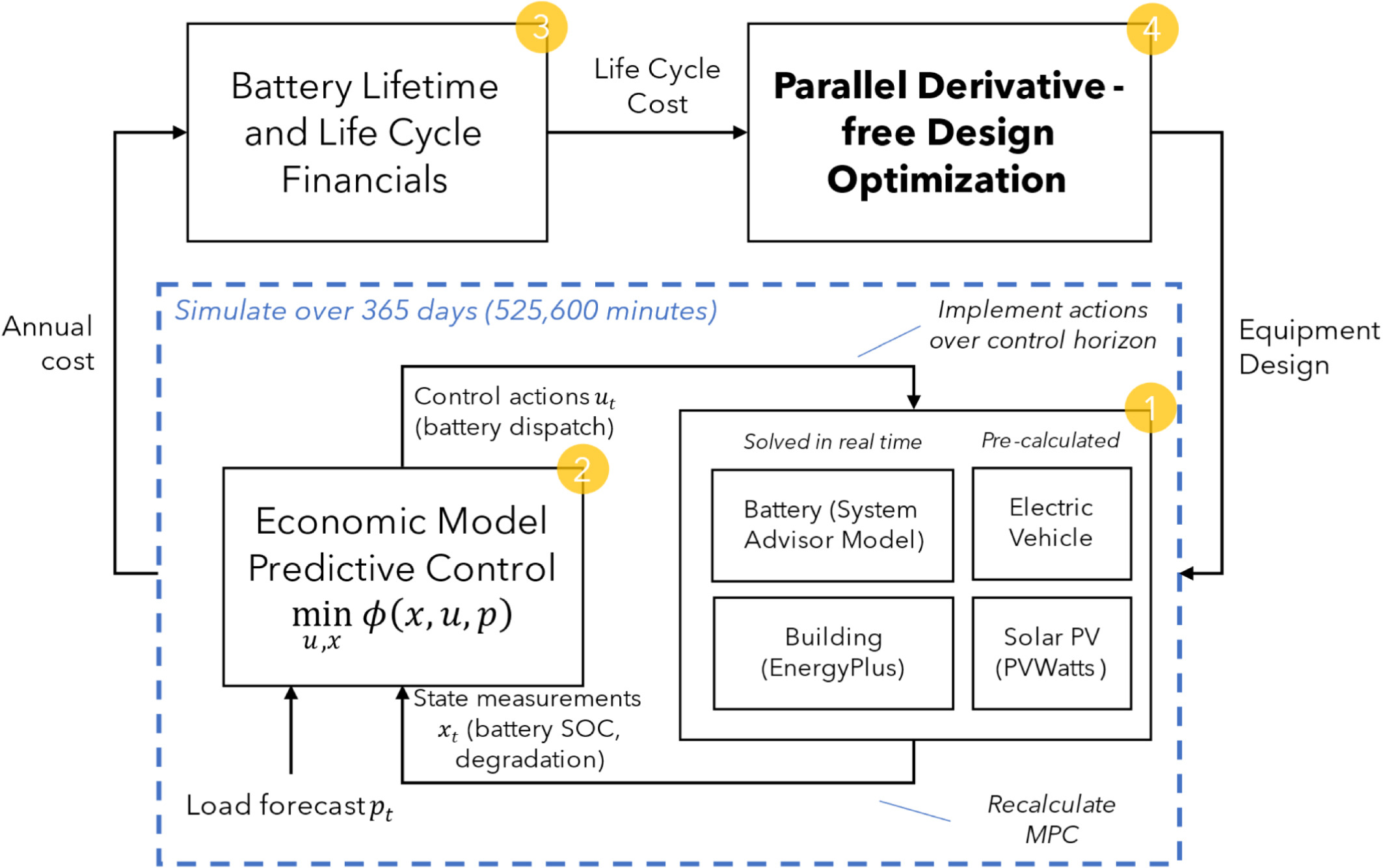
- Parallel derivative-free optimization for simulation-based design of behind-the-meter energy systemsGustavo Campos, Weslley da Silva Pereira, Roberto Vercellino, and 2 more authorsComputers & Chemical Engineering, 2026
In this work, the integrated design and dispatch of behind-the-meter or distributed resources (e.g. stationary battery storage and solar PV generation) is considered. A simulation-based framework is employed, generating high-fidelity results with closed-loop predictive control at a fine resolution, at the expense of high computational cost (several minutes to a few hours per design point). To address this challenge, parallel derivative-free design methods are considered. Four methods are compared, including state-of-the-art surrogate-based methods (Radial-Basis Functions and Gaussian processes) and sampling strategies, an evolutionary-based method, and a simple sequential grid refinement method. As a case study, two types of design problem with increasing complexity are considered, namely, the design of behind-the-meter resources (three design variables) and the inclusion of grid capacity (four design variables). The second yields a constrained design problem for which violations can only be determined after solving the computationally expensive simulation. For the three-dimensional case, all methods present a good performance, achieving a solution within 1% of the optimum after the first iteration, with the sequential grid refinement exhibiting the fastest convergence and achieving the best final objective value. This indicates that the parallel evaluation of multiple sampling points may be more important than the choice of method for small decision spaces. For the four-dimensional constrained case, the Genetic Algorithm presents the best tradeoff between performance and computational effort, while the rough objective function terrain generated by constraint violation penalties reduces the performance of surrogate-based methods. Contour plots with flat regions indicate flexibility in the optimal design and highlight the importance of characterizing the solution space.
2025
-
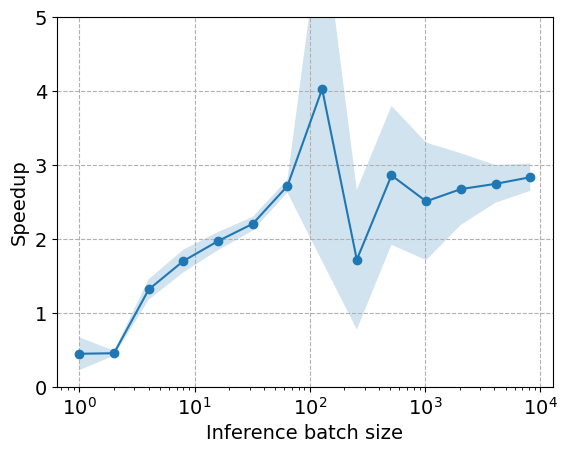 Accelerating Floating-Point Computations with Intel AMXWeslley da Silva Pereira2025
Accelerating Floating-Point Computations with Intel AMXWeslley da Silva Pereira2025Intel AMX is a built-in component of recent Intel CPU architectures, first supported by the Intel Sapphire Rapids in 2023, that enables efficient dense matrix multiplications using mixed precision with low-precision data types. The popularity of mixed-precision algorithms has grown recently, primarily due to their use on GPUs to enhance the efficiency of HPC applications, particularly for the training of large language models. The availability of mixed precision on CPUs represents a cost-effective solution for applications where high speed is not critical. This report shows how to use the Intel AMX accelerator through examples in C++ and Python. The examples will focus on mixed-precision floating-point operations obtained by the use of bfloat16 (or BF16) to accelerate code in single precision. We employ a bottom-up methodology, starting from specific register instructions (TMUL operation) to higher-level applications in libraries such as Intel MKL, PyTorch, and TensorFlow, ensuring a comprehensive understanding of the accelerator’s potential. Additionally, we provide insights into the expected performance gains when leveraging the accelerator on the Kestrel HPC machine at the National Renewable Energy Laboratory.
2024
- Low Precision for Lower Energy ConsumptionWeslley da Silva Pereira, Joao Vitor de Oliveira Silva, and Tokey TahmidIn ASCR Workshop on Energy-Efficient Computing for Science, 2024
Low-precision numeric types offer significant efficiency and energy benefits for computing applications. Mixed-precision algorithms, combining low and high precision types, maintain accuracy while improving performance. Despite advantages, there exist challenges on adapting existing mixed-precision algorithms to new technologies, such as new hardware architectures and new low-precision data types. This paper presents current challenges and opportunities to advance science in this domain targeting more energy efficient solutions.
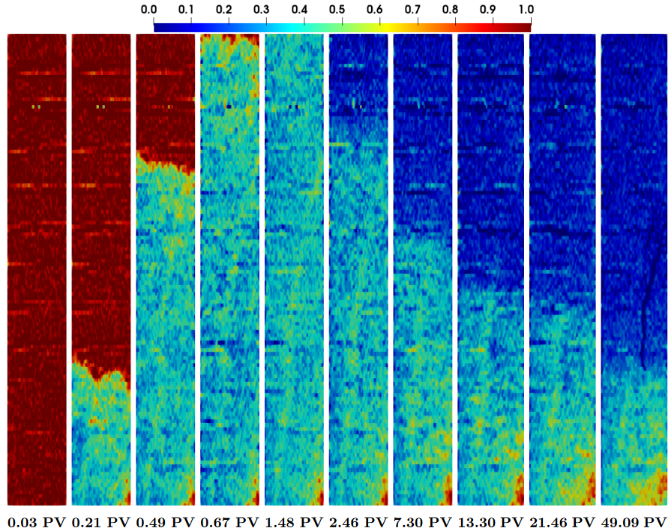
- On Mapping Local Foam Mobility in Porous Media from Computed Tomography DataGrigori Chapiro, Thiago O. Quinelato, Weslley Pereira, and 2 more authorsSPE Journal, Nov 2024
Recovering apparent viscosity and foam texture fields from coreflooding experiments is challenging, even with modern computed tomography (CT) scan equipment. In this work, we present an explicit expression for efficiently calculating effective foam viscosity and propose an improved procedure for processing CT scan images to obtain accurate water saturation profiles. Using these techniques, we processed data from a CT scan of a coreflooding experiment, showing that the increase in effective foam viscosity due to foam generation occurs early during injection and before breakthrough. The fast increment in apparent viscosity is due to foam generation before breakthrough. After breakthrough, foam texture reaches its maximum, and effective foam viscosity grows logarithmically over time as the foamed gas sweeps out the water phase. The pressure drop obtained by using the effective foam viscosity showed good agreement with the experimentally obtained values before breakthrough. The workflow proposed here could be readily adapted to other foam models, provided reasonable estimates for these new quantities can be determined from experiments.
- Low Precision and Efficient Programming Languages for Sustainable AI: Final Report for the Summer Project of 2024Joao Vitor de Oliveira Silva, Tokey Tahmid, and Weslley da Silva Pereira2024
This document contains all relevant material generated during the authors’ summer internship at NREL in 2024. This report shows how to improve energy efficiency of a few code samples by using low-precision data types combined with mixed-precision algorithms. The main applications considered here are (i) linear system solvers using mixed precision, and (ii) neural networks using mixed precision. This report also discusses how programming languages affect energy consumption of algorithms, energy metrics for a code and tools, and the available current software and hardware infrastructure.
2023
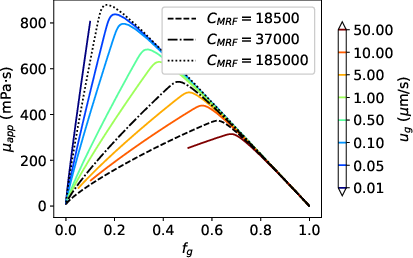
- Traveling Wave Solutions for Non-Newtonian Foam Flow in Porous MediaWeslley da Silva Pereira and Grigori ChapiroTransport in Porous Media, 2023
The injection and in situ generation of foam in porous media successfully control gas mobility and improve the fluids’sweep efficiency inside porous media. Mathematical models describing this problem use two phases, foamed gas, and fluid, and usually have a term for foam generation and destruction. Moreover, the non-Newtonian foam behavior is frequently modeled using Hirasaki and Lawson’s formula for foamed gas viscosity. In this paper, we detail how the traveling wave analysis can be used to estimate the propagation profiles and velocity for a range of non-Newtonian foam models in porous media at constant total superficial flow velocity. We reformulate Hirasaki and Lawson’s formula in an explicit form allowing us to find traveling wave solutions for a foam model with non-Newtonian gas viscosity and a foam generation linearly dependent on the foam texture. Comparing the solution with the one for the Newtonian version allows us to analyze qualitatively and quantitatively the rheology of the foam flow in porous media.
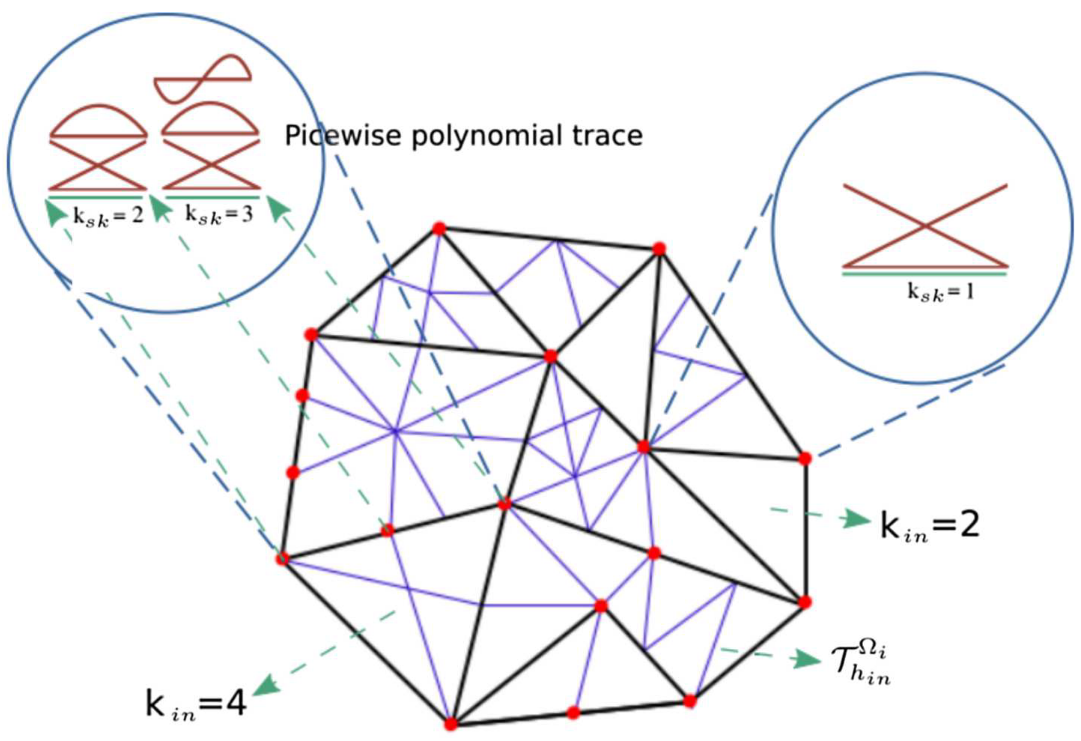
- A Petrov–Galerkin multiscale hybrid-mixed method for the Darcy equation on polytopesHonório Fernando, Larissa Martins, Weslley Pereira, and 1 more authorComputational and Applied Mathematics, 2023
In this work, we propose a new method called Petrov–Galerkin multiscale hybrid-mixed (PGMHM for short) as a variant of the multiscale hybrid-mixed (MHM) method. Its construction starts from a Petrov–Galerkin formulation for the Lagrange multiplier space, defined by enriching the trial spaces with residual-based functions on the partition faces. As a result, jump terms are added to the original MHM method, which penalizes the lack of conformity of MHM numerical solutions. As a consequence of space enrichment, the method induces local post-processing of the numerical solution that incorporates the model’s physical aspects and preserves the exact solution’s local conservation properties. Numerical experiments validate the theoretical results and verify the accuracy of PGMHM on highly heterogeneous problems.
2022
- Proposed Consistent Exception Handling for the BLAS and LAPACKJames Demmel, Jack Dongarra, Mark Gates, and 7 more authorsIn 2022 IEEE/ACM Sixth International Workshop on Software Correctness for HPC Applications (Correctness), 2022
Numerical exceptions, which may be caused by overflow, operations like division by 0 or sqrt(−1), or convergence failures, are unavoidable in many cases, in particular when software is used on unforeseen and difficult inputs. As more aspects of society become automated e.g., self-driving cars, health monitors, and cyber-physical systems more generally, it is becoming increasingly important to design software that is resilient to exceptions, and that responds to them in a consistent way. Consistency is needed to allow users to build higher-level software that is also resilient and consistent (and so on recursively). In this paper we explore the design space of consistent exception handling for the widely used BLAS and LAPACK linear algebra libraries, pointing out a variety of instances of inconsistent exception handling in the current versions, and propose a new design that balances consistency, complexity, ease of use, and performance. Some compromises are needed, because there are preexisting inconsistencies that are outside our control, including in or between existing vendor BLAS implementations, different programming languages, and even compilers for the same programming language. And user requests from our surveys are quite diverse. We also propose our design as a possible model for other numerical software, and welcome comments on our design choices.
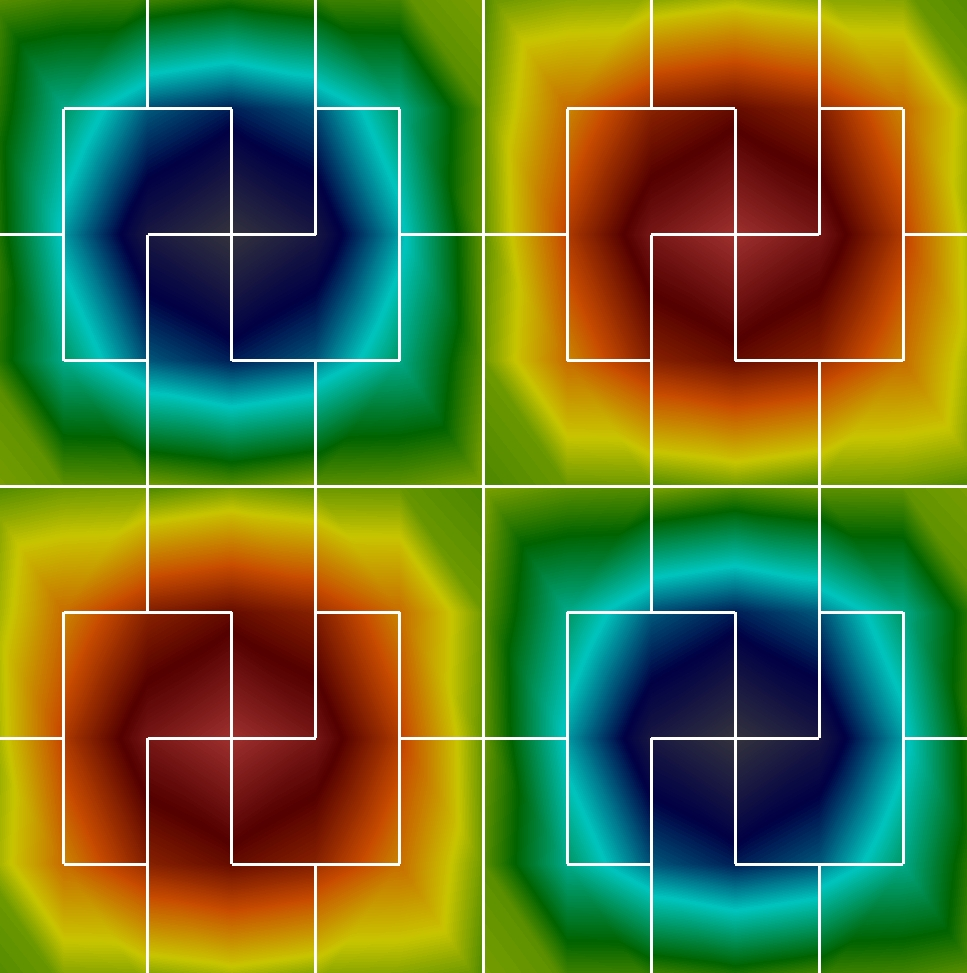
- The MHM Method for Linear Elasticity on Polytopal MeshesAntônio Tadeu A. Gomes, Weslley Pereira, and Frédéric ValentinIMA Journal of Numerical Analysis, Aug 2022
The multiscale hybrid-mixed (MHM) method consists of a multi-level strategy to approximate the solution of boundary value problems with heterogeneous coefficients. In this context, we propose a new family of finite elements for the linear elasticity equation defined on coarse polytopal partitions of the domain. The finite elements rely on face degrees of freedom associated with multiscale bases obtained from local Neumann problems with piecewise polynomial interpolations on faces. We establish sufficient conditions on the fine-scale interpolations such that the MHM method is well-posed and optimally convergent under local regularity conditions. Also, a multi-level error analysis demonstrates that the MHM method achieves convergence without refining the coarse partition. The upshot is that the Poincaré and Korn’s inequalities do not degenerate, and then the convergence arises on general meshes. Two- and three-dimensional numerical tests assess theoretical results and verify the robustness of the method on a multi-layer media case.
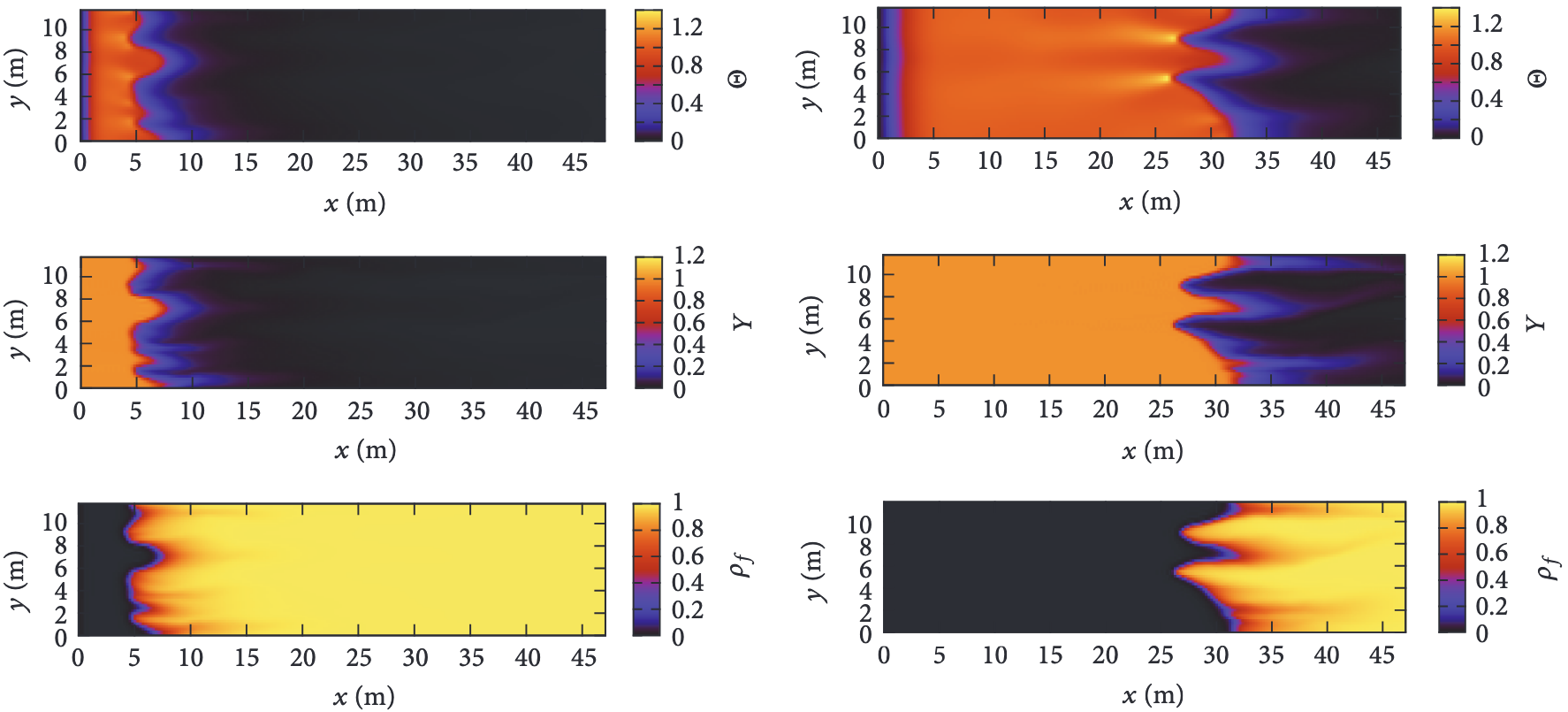
- The traveling wavefront for foam flow in two-layer porous mediaAndrés J. Castrillón Vásquez, Luis Fernando Lozano, Weslley Pereira, and 2 more authorsComputational Geosciences, 2022
The injection of foams into porous media has gained importance as a method of controlling gas mobility. The multilayer structure of the porous medium raises a question on its efficiency in dealing with layers of different permeabilities. The present work shows the existence of a single traveling wavefront in a two-layer porous medium for a simplified model, which was derived from a realistic two-dimensional one. Besides the necessary conditions for the solution’s existence, we prove that the traveling wave velocity is a weighted average of the velocities as if both layers were isolated. All theoretical estimates were validated through one- and two-dimensional simulations. Finally, we estimated the order of magnitude of the characteristic time the traveling wavefront needs to stabilize.
2021
- New H(div)-conforming multiscale hybrid-mixed methods for the elasticity problem on polygonal meshesPhilippe R. B. Devloo, Agnaldo M. Farias, Sônia M. Gomes, and 3 more authorsESAIM: M2AN, 2021
This work proposes a family of multiscale hybrid-mixed methods for the two-dimensional linear elasticity problem on general polygonal meshes. The new methods approximate displacement, stress, and rotation using two-scale discretizations. The first scale level setting consists of approximating the traction variable (Lagrange multiplier) in discontinuous polynomial spaces, and of computing elementwise rigid body modes. In the second level, the methods are made effective by solving completely independent local boundary Neumann elasticity problems written in a mixed form with weak symmetry enforced via the rotation multiplier. Since the finite-dimensional space for the traction variable constraints the local stress approximations, the discrete stress field lies in the H(div) space globally and stays in local equilibrium with external forces. We propose different choices to approximate local problems based on pairs of finite element spaces defined on affine second-level meshes. Those choices generate the family of multiscale finite element methods for which stability and convergence are proved in a unified framework. Notably, we prove that the methods are optimal and high-order convergent in the natural norms. Also, it emerges that the approximate displacement and stress divergence are super-convergent in the L2-norm. Numerical verifications assess theoretical results and highlight the high precision of the new methods on coarse meshes for multilayered heterogeneous material problems.
2017
- Numerical Validation of Analytical Estimates for Propagation of Thermal Waves Generated by Gas-Solid CombustionWeslley da Silva Pereira and Grigori ChapiroGeofluids, 2017
Gas-solid combustion appears in many applications such as in situ combustion, which is a potential technique for oil recovery. Previous work has analyzed traveling wave solutions and obtained analytical formulas describing combustion wave temperature, velocity, and gas velocity for one-dimensional gas-solid combustion model using geometrical singular perturbation theory. In the present work these formulas are generalized. Using numerical simulation we show that they can be adapted and then applied to describe more general two-dimensional models for in situ combustion in a nonhomogeneous porous medium.
2016
- Numerical Solution of a Class of Moving Boundary Problems with a Nonlinear Complementarity ApproachGrigori Chapiro, Angel E. R. Gutierrez, José Herskovits, and 2 more authorsJournal of Optimization Theory and Applications, 2016
Parabolic-type problems, involving a variational complementarity formulation, arise in mathematical models of several applications in Engineering, Economy, Biology and different branches of Physics. These kinds of problems present several analytical and numerical difficulties related, for example, to time evolution and a moving boundary. We present a numerical method that employs a global convergent nonlinear complementarity algorithm for solving a discretized problem at each time step. Space discretization was implemented using both the finite difference implicit scheme and the finite element method. This method is robust and efficient. Although the present method is general, at this stage we only apply it to two one-dimensional examples. One of them involves a parabolic partial differential equation that describes oxygen diffusion problem inside one cell. The second one corresponds to a system of nonlinear differential equations describing an in situ combustion model. Both models are rewritten in the quasi-variational form involving moving boundaries. The numerical results show good agreement when compared to direct numerical simulations.